と。

Github: https://github.com/8-u8

一般線形モデルから一般化線形混合モデルにたどり着くまで

01_統計モデリング 07_R言語

この記事こそが！

R Advent Calendar 22日目の記事です！

このノリがわからない人は前の記事を読んでください。

この前の記事が知る人ぞ知るRおじさんのAtsusyさんなのでこの記事では上がったハードルをくぐっていきます。
皆さん読んできました？省略できちゃうんですよ……これでRとPythonでのギャップが埋まり、世界はデータドリブンに動きますね……

しかも明日はSendaiRの運営をされてる茶畑さん、
あさってはがspoanaの運営をされてるtsuyuponさんの投稿です。

誰？

みなさんご存知きぬいとさんです。 私は学生時代からRを使ってかれこれ8年になりますが、その人生の大半を線形回帰モデルに費やしてきました。
例えば学部時代にはDobsonの一般化線形モデル入門を読んだり、
ベイズモデリングに入門したり、 Stanの可能性に触れたりと、統計モデルの理論を学び、Rで実装し、でてきた数字を眺めるのが私の生きがいなので、今日こそこの話をします。させろ。

ブログでの実装について

ここでソースコードもアレしています。好きに使え。
基本的に疑似データか、Rのオープンなデータでやります。
パッケージはtidyverse、lme4以外はデフォルトです。

github.com

何を書くのか？

この記事では主に以下のことを頑張って書きます。

  • 一般線形モデルの理論
    • Rのlm()関数での実装でできること、結果の解釈。
    • lm()関数でできないこと
  • 一般化線形モデルの理論と実装
    • Rのglm()関数での実装でできること
  • 一般化線形混合モデル
    • 一般化線形混合モデルでできること
    • lme4による実装
    • それってベイズじゃない？

何を書かないのか？

残念なことに以下のことは書いていません。

  • 非線形回帰モデル
  • 正則化回帰モデル
  • 一般化加法的モデル(GAM)
  • 一般化線形混合モデルにおけるパラメータ推定方法

上記のうち正則化回帰モデルについて関連する話は木曜日に書いたので好きに読んでください。

また、今回は「予測精度」ではなく「アンバイアスなパラメータ推定」という目的に特化しています。
もともと統計モデリングの拡張がこの課題への対応として進んできた背景が大きいので。
正直予測っていうのはあまり好きじゃないんですよね。やはり人類は統計データを使って事象の「構造」を旨く捉えようという叡智に挑むべき。やろう。

このあたりの話は実は最近本がでちゃっていて、もうこの本読めばいいんじゃないかって思うんですが泣きながら書きます。

そもそも線型回帰モデルってなんですか？

前提として、我々は「回帰」をどれくらい知っているのでしょう？
ぼくはよく知りませんが、なんでも「ある事象を知りうる情報で予測・説明したい」というモチベーションの時に、
人は「回帰」するといいます *1。
頑張って言うと、ある事象 *2 yを、事象のかたまりXたちの線型結合を使って、以下の問題を解きたいという時に使いがちです。

  • yの構造を明らかにしたい。
  • 観測されていない空間での yの値を予測したい*3

つまり、よく入門書で見る y_i = a + bx_iみたいな形を用いて、 yを xによって「近似」したいというお気持ちです。

よくある質問

Q.線形結合ってなんだよ
A. ググってほしいですが、誤解を恐れずに言うならば「2つのベクトルの内積で表現できる」ってことで許してほしい。

立ち戻って

ぶっちゃけ線型結合であれば別になんでもいいので、以下も線型回帰モデルと呼んでいいらしい。

  • y = a + b x
  • y = a + b_1\sin{x_1} + b_2 \cos{x_2}

結局これらはベクトル (a,b)^Tと計画行列*4 (1,\log{x})^Tとか、 (1, \sin{x_1}, \cos{x_2})の内積として表現できるので線型結合です*5。やったね。

この記事では、予測・構造を明らかにしたい yを「目的変数」と呼び、そのために使いたい事象 Xを「説明変数」と呼びます。このあたりの流儀は人によります*6。まあそんな厳密な話でもないしいっか。次行きます

一般線形モデルの理論

理論つっても \beta = (X^TX)^{-1}X^Tyは絶対出さない*7。
線型回帰モデルは結局のところ、「どんなデータに対してどんなタスクを設定しているか」で使うモデルを考えたほうがよいです。一般線形モデルは今回話すモデルのなかでは一番厳しい仮定を要請します *8。
頻度論的統計学において、GLMMまでの流れは「一般線形モデルの置いている仮定をちょっとずつ外していく」感じです*9。
また、統計モデリングではしばしば「真の構造」的な話をします。
これは統計モデルがあくまで「世界の一部を切り取ったもの」で、本来の事象の構造の近似にすぎないという立場から来ています。実際の風景と絵画や写真との関係性にも喩えられます。
この話はまぁ〜完全に宗派なので、気に食わない場合は仕方ありません。読むのを辞めましょう。

Rだと後述の通り一般線形モデルはlm()関数で実行できます。

一般線形モデルの縛り

では一般線形モデルではどんな制約が与えられているんでしょうか。
一般線形モデルは、モデル式として y = a + bxを扱います*10。
こうしたモデルで得られた予測値を \hat{y}と置くと、「予実のズレ」を計算できます。
統計モデリングの分野では、この「予実のズレ」を「残差」と呼びます。機械学習であれば「誤差」と呼ぶこともありますが、統計モデリングでの「誤差」は、「残差」とは若干異なる意味で使われます。
具体的には、先述した「真の構造」での予実のズレを「誤差」、我々が作ったモデルでの予実のズレを「残差」と呼びます*11。
一般線形モデルは、この「残差」が(標準)正規分布に従うことを要請するモデルです。
この要請を満たすとき、残差の期待値は0になりますし、残差の分布は説明変数と独立であることを示せます。
ここからもわかるように、「切片と説明変数の線形和で説明しきれない部分は、確率的に制御できる」ことをかなり強く要請します。理由は目的が「バイアスのないパラメータ」を推定するためです。

実装

データはtreesを使います。 これは伐採されたブラックチェリーの木の外周(インチ)と、木の高さと重さがデータとして入っています*12。

library(tidyverse)
data("trees")

head(trees, n = 10)

# Girth Height Volume
# 1    8.3     70   10.3
# 2    8.6     65   10.3
# 3    8.8     63   10.2
# 4   10.5     72   16.4
# 5   10.7     81   18.8
# 6   10.8     83   19.7
# 7   11.0     66   15.6
# 8   11.0     75   18.2
# 9   11.1     80   22.6
# 10  11.2     75   19.9

このデータのGirth(周囲の長さ)をHeightで回帰してみましょう。

model_lm <- lm(Girth ~ Height, data = trees)
summary(model_lm)
# Call:
#   lm(formula = Girth ~ Height, data = trees)
# 
# Residuals:
#   Min      1Q  Median      3Q     Max 
# -4.2386 -1.9205 -0.0714  2.7450  4.5384 
# 
# Coefficients:
#               Estimate Std. Error t value Pr(>|t|)   
# (Intercept) -6.18839    5.96020  -1.038  0.30772   
# Height       0.25575    0.07816   3.272  0.00276 **
#   ---
#   Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
# 
# Residual standard error: 2.728 on 29 degrees of freedom
# Multiple R-squared:  0.2697, Adjusted R-squared:  0.2445 
# F-statistic: 10.71 on 1 and 29 DF,  p-value: 0.002758

でましたァ……

読み方がわからないなら教えます。
R advent calendar17日目の記事にも事細かに書いています。
あれ？ここで書く必要はないのでは？
Residualsは残差です。これの平均が0であればよい、ということになります。
Rでは中央値がでていますが、まあまあ0に近い、といっていいかもしれません。
でもちょっと無視するにはでかすぎる……?
ともあれ、最大値〜最小値が左右対称っぽいあたり、「残差が正規分布している」仮定は概ね満たされている、とも考えられますね。
Coefficientsの項が回帰係数に関する情報です。(Intercept)が切片、先の式のaに相当します。
4つ数値が並んでいます。Estimateが推定値ですが、Std.Errorは標準誤差です。これは、推定値がどれだけの範囲を撮りうるかを(ざっくりと)意味します。
t valueは、回帰係数の有意性検定の検定統計量です。P(>|t|)は有意水準で、0に近ければ近いほど良いです*13。 Heightの項を見ると、0.255となり、有意水準0.01の水準で統計的に「0でない」ことが統計的に保証されています。
下の方にあるResidual standard errorは残差の標準誤差です。
こいつが小さければ小さいほど都合は良いのですが、ちょっと大きめ……？
その下のR-squaredは[tex: R2]、つまりは決定係数です。モデルの適合度を意味します。単回帰ではまあこんなもんでしょう。 F-statisticsはモデル全体において「すべての回帰係数が0である」という帰無仮説のもと検定を行った結果です。基本的にまともなモデルなら有意になっています。
Residualsをみると、やはり広く線形回帰は、目的変数と説明変数の「値の大きさ」や「偏り」に大きく依存します*14。
そこで標準化をしてみましょう。例えば下記のように。

use_trees <- trees %>%
  scale() %>% 
  as.data.frame()

Rはscale()関数がデフォルトで実装されており、一瞬で標準化ができます。
Pythonでもsklearn.preprocessing.StandardScaler()などで可能です。
結果は下記。

model_lm_scaled <- lm(Girth ~ Height, data = use_trees)
summary(model_lm_scaled)

# Call:
#   lm(formula = Girth ~ Height, data = use_trees)
# 
# Residuals:
#       Min       1Q   Median       3Q      Max 
# -1.35068 -0.61199 -0.02274  0.87472  1.44621 
# 
# Coefficients:
#               Estimate Std. Error t value Pr(>|t|)   
# (Intercept) 1.890e-16  1.561e-01   0.000  1.00000   
# Height      5.193e-01  1.587e-01   3.272  0.00276 **
#   ---
#   Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
# 
# Residual standard error: 0.8692 on 29 degrees of freedom
# Multiple R-squared:  0.2697, Adjusted R-squared:  0.2445 
# F-statistic: 10.71 on 1 and 29 DF,  p-value: 0.002758

確認してみると、残差の中央値が小さく、標準誤差も小さくなりました。
回帰係数も大きくなり、ました。一方で検定統計量たちは変化ありません。

回帰直線がみてみたい？

plot_point_scaled <- ggplot2::ggplot(data = use_trees, aes(x = Height, y = Girth)) +
  ggplot2::geom_point() + 
  ggplot2::stat_smooth(method = "lm", se = F)
plot_point_scaled

f:id:kinuit:20191221030247p:plain

一般化線形モデルの理論

割と一般線形モデルも使えます。
一方で一般線形モデルでは、以下のデータに対してはあんまりよい結果をもたらしません。

  • 目的変数が0または1をとるとき
  • 目的変数が0以上の整数をとるとき

理由は単純で、目的変数の分布構造が特殊だからです。
例えば一般線形モデルを使って、皆さんご存知タイタニックデータにおいて、生き残ったかどうかを予測することも、生き残った人がどんな人だったのかということを説明することも、あまりよいことではないです。
また、例えば「1日の商品Aの売上」などを「そのまま」目的変数に用いようとする場合も、一般線形モデルでは十分に適合しません。
こうした問題に対応するために、一般線形モデルを拡張します。
一般線形モデルは残差の分布が正規分布に限られていましたが、一般化線形モデルとしてこれを「正規分布以外」に拡張します*15。
拡張の方針は、$a + bx$という線型結合を「リンク関数」という関数を通して$y$に関連付けます。
ロジスティック回帰は代表的な一般化線形モデルですが、その名前もリンク関数がロジットリンク関数であるからです。 このブログでは、一旦ロジスティック回帰をします。

実装

都合よく作ったデータを使います。
使うだけなのでちょっと削りますが。

library(tidyverse)
set.seed(1234)

UseData <- matrix(0,300,10) %>% data.frame()
for(i in 1:ncol(UseData)) {
  UseData[,i] <- runif(nrow(UseData)) + rpois(nrow(UseData), rgamma(nrow(UseData),shape = 1))
}
glm_data <- UseData %>% scale() %>% data.frame()

## 正解のパラメータを置く。
fact <-  3 * glm_data$X10 + 6 * glm_data$X3 + 2 * glm_data$X5
fact <-1/(1 + 3*exp(-fact))  # ロジット変換

glm_data$y <- 0
for(i in 1:nrow(glm_data)){
    # ロジット変換したfactを確率とみなして乱数をぶっこむ
    glm_data$y[i] <- rbinom(1, 1, fact[i])
}

# 見栄えの問題。
glm_data <- glm_data %>% 
   dplyr::arrange(y)

glm_model <- glm(y ~ . ,data = glm_data, family = binomial("logit"))
glm_model %>% summary

# Call:
#   glm(formula = y ~ ., family = binomial("logit"), data = glm_data)
# 
# Deviance Residuals: 
#   Min        1Q    Median        3Q       Max  
# -2.79723  -0.17374  -0.02177   0.01670   2.18644  
# 
# Coefficients:
#               Estimate Std. Error z value Pr(>|z|)    
# (Intercept) -1.16230    0.30015  -3.872 0.000108 ***
# X1           0.06391    0.28657   0.223 0.823517    
# X2          -0.08146    0.25308  -0.322 0.747532    
# X3           6.42789    1.02494   6.271 3.58e-10 ***
# X4           0.39690    0.26543   1.495 0.134826    
# X5           2.24315    0.39967   5.612 1.99e-08 ***
# X6           0.27260    0.29696   0.918 0.358641    
# X7          -0.08142    0.23464  -0.347 0.728589    
# X8           0.05814    0.27094   0.215 0.830100    
# X9           0.04441    0.28057   0.158 0.874241    
# X10          3.32751    0.54027   6.159 7.32e-10 ***
#   ---
#   Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
# 
# (Dispersion parameter for binomial family taken to be 1)
# 
# Null deviance: 392.051  on 299  degrees of freedom
# Residual deviance:  95.277  on 289  degrees of freedom
# AIC: 117.28
# 
# Number of Fisher Scoring iterations: 8

うまく行ったようです。
基本的な見方は一般線形モデルと同じです。
ResidualsがDeviance Residualsに変わっています。これは「逸脱度」と呼ばれており、一般線形モデルにおける残差です。
ロジスティック回帰では目的変数が2値なので、単純な残差(二乗誤差)の計算ではなく、ロジット変換を行った上でのズレを評価することでズレの度合いを評価します*16。 今回はX3、X5、X10を使って目的変数を無理やり設計したのですが、多少のズレはあっても、係数にした値に近い結果がでています。
下の方にAICとでていますが、ロジスティック回帰(というか一般化線形モデル)では決定係数を(厳密に)計算することができないので、適合度規準の一つとして用いられます*17

可視化？

glm_plot <- ggplot2::ggplot(data = glm_data, aes(x = X3, y = y)) +
  geom_point()+
  stat_smooth(method = "glm",method.args = list(family = "binomial"),se = F)  
glm_plot

f:id:kinuit:20191221030324p:plain

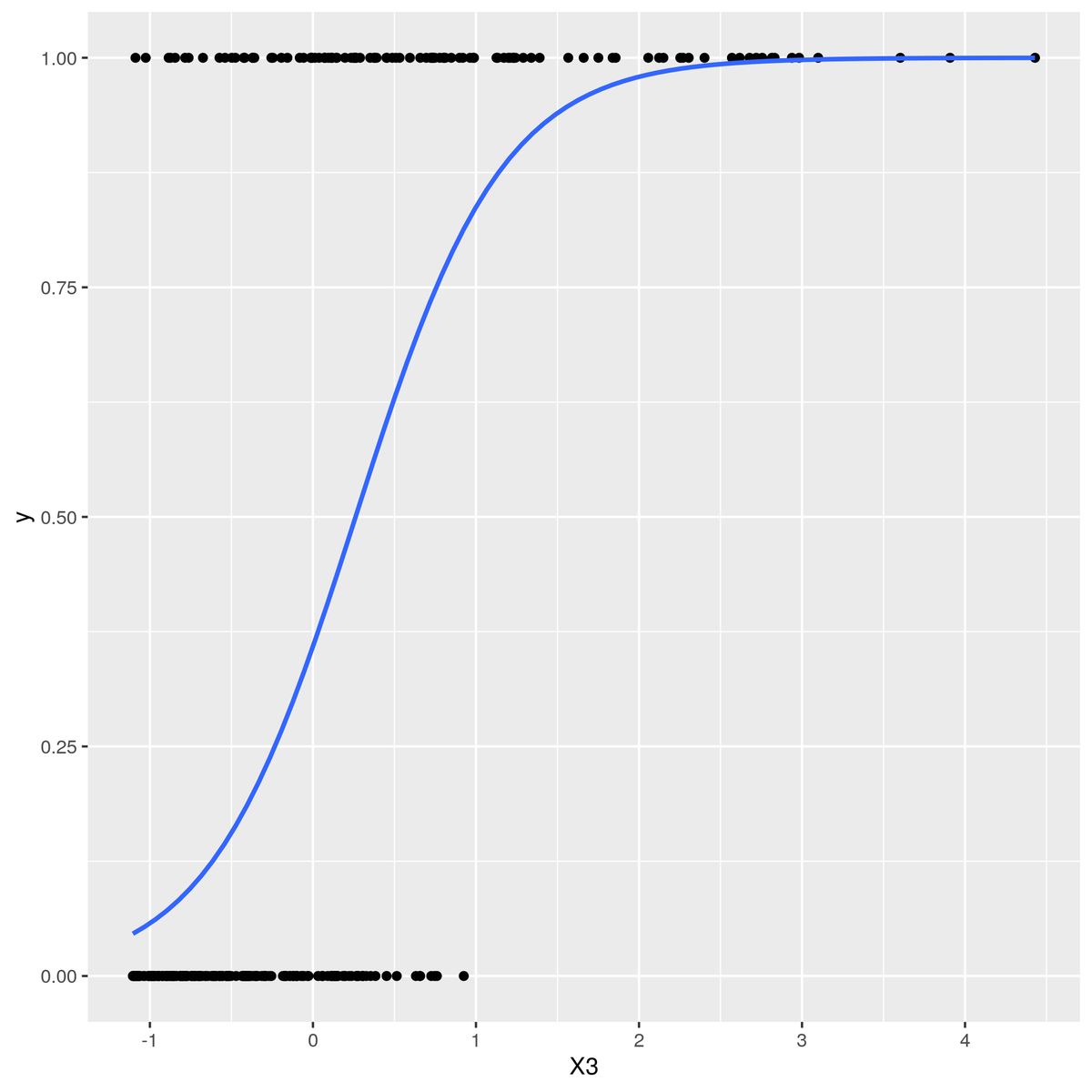
一般化線形混合モデルのお気持ち

一般化線形モデルによって、いろいろなデータを使えるようになりました。
しかし、人は強欲なものです。例えば以下のような場合、一般化線形モデルはそれを説明する術を持ちません。

  • ポアソン回帰において、店舗ごとに集めた日次のデータ1年分で1日の売上を説明したい。
  • ロジスティック回帰において、特定のカテゴリ別に生存予測・説明をしたい
  • 0がめちゃくちゃ多い不均衡データに対してのモデリングをしたい。

これらの問題は「ある変数によって仮定している分布のパラメータが違うんじゃない？」という話に帰着します。
「人によって違うじゃない！」と言うやつです。困りました。
これに対して一般化線形混合モデルは、仮定する分布をさらに拡張して、パラメータが既知の混合分布なら使えるようにします*18。
「混合分布」は、「確率分布Aと確率分布Bを混ぜたやつ」みたいな感じです。
代表的な混合分布に負の二項分布があります。これはポアソン分布のパラメータ$\lambda$がガンマ分布に従うと仮定して拡張した分布としての定義があります*19。

せっかくなのでデータも作ります。

library(lme4)
library(tidyverse)
set.seed(1234)

x <- c(abs(rnorm(20, 3, 4)),
       abs(rnorm(30, 0, 1)),
       abs(rnorm(50, 6, 4))
       )
cat <- c(rep(1,20), rep(2,30), rep(3,50))
y <- numeric(100)
gam <- numeric(100)
for(i in 1:20){
  gam[i] <- rgamma(1, shape = 4 * x[i]) + 0
  y[i]   <- rpois(1, gam[i])
}
for(i in 21:30){
  gam[i] <- rgamma(1, shape =  4 * x[i]) + 5.0
  y[i]   <- rpois(1, gam[i])
}
for(i in 31:50){
  gam[i] <- rgamma(1, shape = 4*x[i]) + 10
  y[i]   <- rpois(1, gam[i])
}

usedata <- data.frame(y = y, x = x, cat = cat)

usedata %>% summary

usedata$y %>% var   # 96.00919
usedata$y %>% mean  # 6.03

ポアソン分布についてのお話はしていませんでした。
ポアソン分布は「0以上の整数をとり、平均と分散が同じ値になる分布」です。
一方で、今回生成したデータは平均と分散が一致しません。これを過分散(Overdispersion)と呼びます。
こういう時には単純なポアソン回帰と言うよりは、何らかの混合分布を残差に置いたほうが良いだろう、と考えます。
何なら今回のデータ、 xの生成過程が違って、それに応じてyのパラメータもちょっとずつ違うっぽく作っています。

比較したいしポアソン回帰も実行します。

model_pois <- glm(y ~ x, data = usedata, family = "poisson")
summary(model_pois)
# Call:
#   glm(formula = y ~ x, family = "poisson", data = usedata)
# 
# Deviance Residuals: 
#   Min      1Q  Median      3Q     Max  
# -3.808  -3.337  -2.759   0.787  15.643  
# 
# Coefficients:
#   Estimate Std. Error z value Pr(>|z|)    
# (Intercept)  1.98627    0.05586  35.557  < 2e-16 ***
#   x           -0.05012    0.01118  -4.484 7.34e-06 ***
#   ---
#   Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
# 
# (Dispersion parameter for poisson family taken to be 1)
# 
# Null deviance: 1233.5  on 99  degrees of freedom
# Residual deviance: 1211.7  on 98  degrees of freedom
# AIC: 1411.3
# 
# Number of Fisher Scoring iterations: 7
model_lme4 <- lme4::glmer.nb(y ~ x + (1|cat), data = usedata)
summary(model_lme4)

# Generalized linear mixed model fit by maximum likelihood (Laplace Approximation) ['glmerMod']
# Family: Negative Binomial(7.0696)  ( log )
# Formula: y ~ x + (1 | cat)
# Data: usedata
# 
# AIC      BIC   logLik deviance df.resid 
# 323.2    333.7   -157.6    315.2       96 
# 
# Scaled residuals: 
#   Min       1Q   Median       3Q      Max 
# -1.69248 -0.13224 -0.03589 -0.01440  2.13598 
# 
# Random effects:
#   Groups Name        Variance Std.Dev.
# cat    (Intercept) 32.78    5.726   
# Number of obs: 100, groups:  cat, 3
# 
# Fixed effects:
#   Estimate Std. Error z value Pr(>|z|)    
# (Intercept)  -2.3935     3.6930  -0.648    0.517    
# x             0.3068     0.0376   8.160 3.35e-16 ***
#   ---
#   Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
# 
# Correlation of Fixed Effects:
#   (Intr)
# x -0.070

どちらも回帰係数は統計的に有意ですが、lme4::glmer.nbでの推定のほうが、AICや逸脱度などを見ると、ポアソン回帰の結果よりも改善していることが確認できます。
GLMMでの特徴は、モデルを「ランダム効果」と「固定効果」に分ける点です。
今回はデータの設計上切片がcat変数によって異なるという前提で(つまりxの傾きはcatによらず一定)で回しました*20。

え？可視化？

result <- data.frame(res_lme4 = expm1(predict(model_lme4)),
                     res_pois = expm1(predict(model_pois)),
                     y        = usedata$y)
plot_pois <- ggplot2::ggplot(data = result, aes(x = res_pois, y)) + geom_point()
plot_lme4 <- ggplot2::ggplot(data = result, aes(x = res_lme4, y)) + geom_point()
plot_lme4_fix <- plot_lme4 + xlim(c(0,40))
plot_pois

ポアソン回帰。 なんかもうひどい。

f:id:kinuit:20191221041100p:plain

ポアソン・ガンマ回帰

f:id:kinuit:20191221041124p:plain

ちょっとばびゅーんってなってるなあ。

f:id:kinuit:20191221041200p:plain

スケール詰めるとマシか((本当はcat別に色でも分けりゃいいんですが諦めました(それでいいの？)))

さらにその先へ――

一般化線形混合モデルは「パラメータが既知」の混合分布にまで拡張します。人はこう考えるわけです。

「別に分布が既知である必要もないのでは？」

なんて強欲な！推定する分布がわからなかったらなんのパラメータを推定すればいいかわからないじゃないか！

これを解決するためには頻度論から脱出しなければなりません。階層ベイズモデルです。
階層ベイズモデルであれば、階層構造別に事前分布さえ設定すれば、結局事後分布の構造に要請するべき仮定はありません。
事前分布も共役な〜とかいいつつも、頑張ればどんな分布を置いても基本死にはしません((かなり暴力的に申し上げてます)))。
今回この話はしません。間に合わなかったわけじゃないです。間に合わなかったわけじゃないです。

おわりに

長くなりました。このブログ史上最大の規模です。
この記事では一般線形モデルから一般化線形混合モデルまでを雑に、語弊を恐れずに辿ってきました。
統計モデリングは「データの構造や分析の目的に応じて、どんな仮定を受け入れられるか」というところからスタートしています。
少しずつ仮定を外していって、柔軟なモデルを作っていく流れは、個人的には好きだなあと思います。
また、R言語による回帰分析の結果の読み取り方に割と文字を割いた自覚があります。
回帰分析回しても、結果が読み取れなかったり、推定値が信頼できるものなのか、統計的に意味のあるものなのかを読み取れないという話は
身近では聞かないのですが、まあこういう話を記録する分にはいいのかなあと思います。 この記事の範囲で話していないことに以下のようなトピックがあります。

  • 不偏性・一致性などの「パラメータの望ましい性質」
    • パラメータのバイアスって何なのか
    • 多重共線性
  • 交互作用項
  • 因果推論系の回帰問題

モデルの拡張以前に、こうした問題は「バイアスなくパラメータを推定する」という「構造理解」の文脈では避けられないトピックで、こういう話をちゃんとすることは重要です。
ただこれらの話はRの話から大きく外れちゃうので、また別の記事で書こうと思います。

*1:もともとregressionって「退行」とか「後退」とか「逆行」意味するらしいですよ。誤解を恐れずに言うならば、結果から原因のパラメータを推定する操作にも見えるので、そういう意図をもった単語だったのかもですね。

*2:ここで「事象」と呼んでいるのは正直「結果」って言うと因果推論みが出てきてつらいからです

*3:空間とは地理空間でも時間空間でもなんでもいいです。

*4:ちょっと語弊がありますが知りません(は？)。

*5:結局出力 yが入力 Xの一次関数となっていればいい

*6:きぬいとの古巣ではyを「従属変数」 Xを「独立変数」とか呼んでました。機械学習界隈では「出力」「入力」と呼ぶ人もいるでしょう。

*7:線形モデルにおける解

*8:これはあくまで目的変数と説明変数に対する要請で、線型回帰モデルを解く場合は別の仮定を要請します。具体的には最小二乗法を解くための仮定や最尤法を解くための仮定とは、ここで要請している仮定は別のお話だと思ってください。

*9:Fateが好きな人はあの聖槍ロンゴミニアドに与えられている拘束を1個ずつ外していくことで威力を上げていくみたいなイメージをもってくれればいいと思います。僕は上父上がほしい。

*10:このブログでは一般線形モデルは主に重回帰分析を代表的に取り扱いますが、分散分析やt検定などにも応用されます。

*11:https://bellcurve.jp/statistics/course/9704.html

*12:https://www.trifields.jp/r-sample-data-491

*13:回帰係数の有意性は、「その回帰係数が0である」という帰無仮説を棄却できるかどうかの規準となります

*14:ニューラルネットワークとかGAMとかでも依存します。

*15:具体的には指数型分布族全般に拡張します。具体的な拡張は原著を確認してみてください。

*16:例えばこのサイトが詳しいです

*17:細かい話をすれば疑似決定係数などを計算することは可能ですが、今回は省略します。

*18:この辺実は未知でもいいのかな。教えて欲しさ。

*19:Poisson-Gamma Mixture

*20:実はこのレベルだとglm.nb関数でもできてしまいますが、
切片だけじゃなく傾きにもランダム効果を設けたいときは、lme4で回ります